Problem #33

A Senate committee has $5$ Democrats, $5$ Republicans, and $1$ Independent. In how many ways can they sit around a circular table if all the members of each party all sit next to each other? (Two seatings are considered equivalent if one is a rotation of the other.)

Correct answer gets 20 PP.

Problem #32-Solved by Walter Li

What is $123_5+123_5$?

Problem #31-Solved by Walter LI

How many zeros does $10!$ end with when expressed in base $11$?

Problem #30

How many rectangles are there in the Cartesian plane with center at the origin, all four vertices with integer coordinates, and a diagonal of length $20$?

Correct answer gets a grand prize of 50 PP.

Problem #29-Solved by Walter Li

Let $\log_4 3=x$. Then $\log_2 27=kx$. Find $k$.

Problem #28-Solved by Peter Dun

Find all values of $x$ that satisfy the equation $x=\sqrt{11-2x}+4$.

Problem #27

If $60^a=3$ and $60^b=5$, then what is $12^{[(1-a-b)/2(1-b)]$?

Correct answer gets a grand prize of 50 PP.

Problem #26

Find the area of $|ax+b|+|cy+d|\le e$ in terms of $a, b, c, d,$ and $e$.

Correct answer gets a grand prize of 50 PP.

Problem #25-Solved by Peter Dun

I went to my favorite taco stand with some friends. Between us we bought $6$ tacos and $2$ burritos, and I noticed that the ratio of the amount we spent on tacos to the amount we spent on burritos was $7:4$. Later we went back and bought $4$ tacos and $3$ burritos and spent $1$ dollar less. How much money did we spent that time?

Problem #24-Solved by Peter Dun

Find all positive integer values of $c$ such that the equation $x^2-7x+c=0$ only have roots that are real and rational.

Problem #23-Solved by Peter Dun

A club has $10$ members, $5$ boys and $5$ girls. Two of the members are chosen at random. What is the probability that they are both girls?

Problem #22-Solved by Peter Dun

A small car company operates machinery for $t$ hours per day that produces $c$ cars per hour, where $c$ and $t$ are positive integers. After upgrading the machinery, the company can now produce$2c+5$ cars per hour. If the machinery now operates for $t-2$ hours per day and yet produces the same number of cars per day, how many cars per day does it produce?

Problem #21-Solved by Peter Dun

Find the sum of all whole numbers $x$ that satisfy $x+\frac{25}{x}=10$.

Problem #20-Solved by function

Find the largest integer $n$ such that $n$ has exactly $4$ positive divisors and $n$ divides $100!$.

Problem #19-Solved by Peter Dun

If the diagonal of a cube is $5$, what is the volume of the cube? Express your answer in simplest radical form.

Problem #18-Solved by Peter Dun

Find a $3$-digit palindrome where the square of the product of the digits equals the sum of the digits.

Problem #17-Solved by Peter Dun

What is the area of the region defined by $|x-12|+|2y+5|\le7$?

Problem #16-Solved by function

Parabola needs to catch a train. The train arrives randomly some time between 1:00 and 2:00, waits for $10$ minutes, and then leaves. If Parabola also arrives randomly between 1:00 and 2:00, what is the probability that the train will be there when Parabola arrives?


This problem is extra hard, so the correct answer gets $20$ PP.

Problem #15-Solved by Peter Dun

What is the least number that has a remainder of $1$ when divided by the first $8$ positive integers?

Problem #14-Solved by function

If an integer greater than $1$ raised to the $\frac{1}{2}$, $\frac{1}{3}$, and $\frac{1}{4}$ power remains an integer, what is the least possible integer that satisfies these conditions?

Problem #13-Solved by function

Given that a chord of length 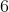divides a circle, A, of radius 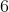into two distinct regions, what is the area of the larger region?

Riddle #6-Solved by Josh Pan

A hunter shoots a bird from a tree with 3 birds. How many birds are left?

Problem #12-Solved by Walter Li

Given a circle with radius 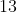and a chord of length 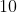, find the length of the segment with a question mark that is perpendicular to the chord.

Problem #11-Solved by Walter Li

How many different flavors of ice cream are needed for different 4-scoop cones?

Problem #10-Solved by Walter Li

How many integers between and contain both the digits and ?

Problem #9-Solved by Kyle Peters

If , then what is?

Problem #8-Solved by function

What is the sum of the numbers that each one of them is more than its reciprocal?

Problem #7-Solved by function

The side length of a square is 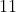cm long. The midpoints of each sides are joined to form a second square. The process of joining the midpoints of the sides of the innermost square is repeated. What is the number of square centimeters in the area of the 6th square? Give your answer as a common fraction in lowest terms.

Riddle #5-Solved by Josh Pan

Referring to Riddle #4, what is the most expensive store in America?

Riddle #4-Solved by Josh Pan

What is the most abused single digit in America?

Riddle #3-Solved by function

Besides log function, what else brings the power down?

Riddle #2-Solved by Vy Tran

I'm as big as an elephant, but lighter than a feather. What am I?

Riddle #1-Solved by Vy Tran

What stinks while living, but in death, smells good?

Problem #6-Solved by Josh Pan

If and and then what is the average of and?

Problem #5-Solved by function

How many ways are there for Victor, Alex, Austin, Derek, and Harrison to sit in a row if Victor and Harrison hate each other so much they can't sit next to each other?

Problem #4-Solved by function

If there are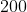Victors in 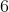Davids, and 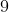Davids in Joshies, then how many Victors are in a Joshy? Express your answer as a common fraction.

Problem #3-Solved by Josh Pan

If there are 5 Victors in 2 Alexs, and 4 Alexs in 3 Austins, and 2 Austins in 6 Adams, and 7 Adams in 3 Harrisons, and 4 Harrisons in 54 Wills, then how many Victors equals 94 Wills?

Problem #2-Solved by Josh Pan

There are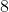women of different heights at a party. Every person will only shake hands with someone shorter than herself. How many handshakes will take place?

Problem #1-Solved by Josh Pan

people attend a party. Each person shakes hands with at least one other person. What is the minimum possible number of handshakes?

Solving Problems

To solve a problem, please comment and put your name that you want to be called and the answer you have.